直流电机的正弦换向是什么?
尽管理论上无刷直流(BLDC)电动机的反电动势波形是梯形的,但实际上,电动机中的电感会使反电动势平滑为更正弦的形状。这就是BLDC电机可以使用梯形或正弦换相方法的原因。虽然梯形换向是这两种方法中比较简单的一种,但它在每个换向步骤(每60度)都会产生明显的转矩波动。正弦换向可消除梯形换向固有的转矩脉动,并提供平稳的运动和精确的电机控制。
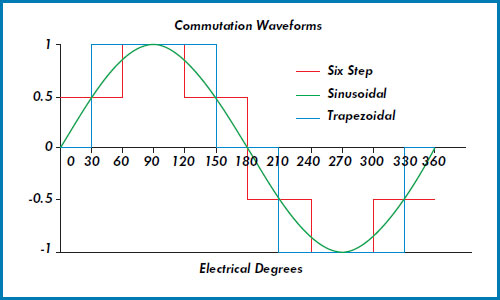
正弦换向可消除梯形或六步法(也称为“改进梯形”)方法产生的转矩脉动。
图片来源:Aerotech Inc.
正弦换向的基本前提是为每个电动机绕组提供随着电动机旋转而呈正弦变化的电流。电流相移120度,以匹配定子绕组的方向。当前空间矢量的大小恒定,并且始终与转子正交。(回想一下,当定子和转子磁场相互正交或成90度时,就会产生最大转矩。)实现正弦换向的关键是准确确定转子位置的能力。由于霍尔设备仅提供转子位置的粗略测量,因此通常使用编码器来提供转子位置信息。
根据转子位置,创建两个正弦波形,彼此相移120度。将这些信号乘以扭矩命令可产生与所需扭矩成比例的振幅。这些命令被馈送到控制器,该控制器调节电动机绕组中的电流。根据基尔霍夫电流定律,这三个电流的总和必须等于零,因此,第三个电动机绕组中的电流是前两个电流的负总和(保持三个电流的总和为零),因此不能为直接控制。
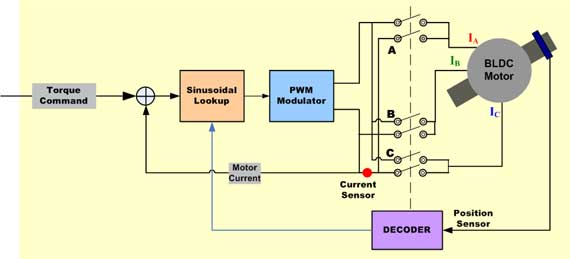
BLDC电动机的正弦换向框图。
图片来源:瑞萨电子公司
为了了解其工作原理,让我们看一下三相电动机的转矩方程:
T = Kt * [I A * Sin(θ)+ I B * Sin(θ+120)+ I C * Sin(θ+240)]
这里:
T =扭矩
Kt =扭矩常数
I A,I B,I C =相电流
θ=轴电角度
由于相电流是正弦的:
I A = M * Sin(θ)
I B = M * Sin(θ+ 120)
I C = M * Sin(θ+ 240)
其中M =相对于角度θ的电动机电流指令
代入,我们得到:
T = Kt * M * [(sin 2(θ)+ sin 2(θ+ 120)+ sin 2(θ+ 240)]
求解三角函数*给我们:
T = Kt * M * 1.5 * [sin 2(θ)+ cos 2(θ)]
由于sin 2(θ)+ cos 2(θ)= 1,因此该方程式简化为:
T = 1.5 * Kt * M
这表明扭矩与轴角无关,从而消除了扭矩波动。
正弦换向的不利之处在于它在高速下效率低下。电机旋转得越快,正弦信号的频率就越高,并且控制器很难跟踪这些高频信号。较高的电动机速度还会导致反电动势的振幅和频率都增加,从而使电动机更难以克服。
这两种情况都会对电流控制环路造成干扰,并导致相位滞后和电流误差。结果是,当前空间矢量相对于转子从理想(正交)位置移开,并且给定电流量产生的转矩较小。
TAG 直流电机







